2.1线性表概述
表也可以说是线性表,名为线性存储结构。使用线性表存储数据的方式可以这样理解,即“把所有数据用一根线儿串起来,再存储到物理空间中”。

如上图所示,这是一组具有“一对一”关系的数据,我们接下来采用线性表将其储存到物理空间中。
首先,用“一根线儿”把它们按照顺序“串”起来,如下图所示:
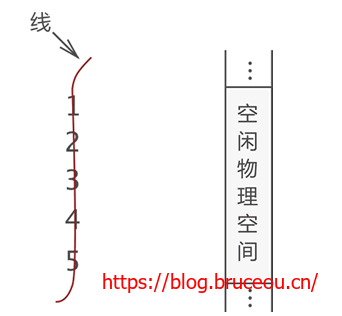
上图中,左侧是“串”起来的数据,右侧是空闲的物理空间。把这“一串儿”数据放置到物理空间,我们可以选择以下两种方式,如下图所示。
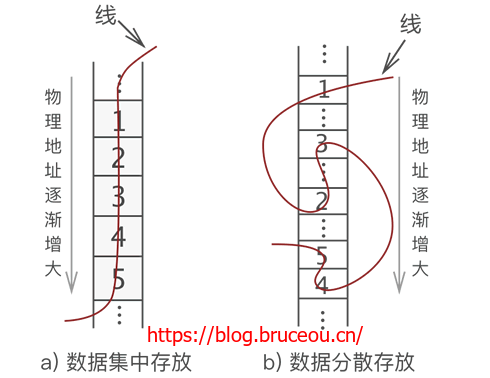
图 a) 是多数人想到的存储方式,而图 b) 却少有人想到。我们知道,数据存储的成功与否,取决于是否能将数据完整地复原成它本来的样子。如果把图 a) 和图 b) 线的一头扯起,你会发现数据的位置依旧没有发生改变。因此可以认定,这两种存储方式都是正确的。
将具有“一对一”关系的数据“线性”地存储到物理空间中,这种存储结构就称为线性存储结构(简称线性表)。
使用线性表存储的数据,如同向数组中存储数据那样,要求数据类型必须一致,也就是说,线性表存储的数据,要么全不都是整形,要么全部都是字符串。一半是整形,另一半是字符串的一组数据无法使用线性表存储。
线性表存储数据可细分为以下 2 种:
- 如图 a) 所示,将数据依次存储在连续的整块物理空间中,这种存储结构称为顺序存储结构(简称顺序表);
- 如图 b) 所示,数据分散的存储在物理空间中,通过一根线保存着它们之间的逻辑关系,这种存储结构称为链式存储结构(简称链表);
也就是说,线性表存储结构可细分为顺序存储结构和链式存储结构。
数据结构中,一组数据中的每个个体被称为“数据元素”(简称“元素”)。
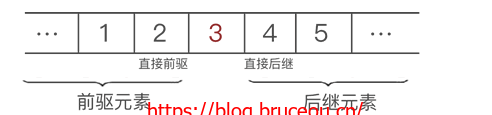
- 某一元素的左侧相邻元素称为“直接前驱”,位于此元素左侧的所有元素都统称为“前驱元素”;
-
某一元素的右侧相邻元素称为“直接后继”,位于此元素右侧的所有元素都统称为“后继元素”;
下图数据中的元素 3 来说,它的直接前驱是 2 ,此元素的前驱元素有 2 个,分别是 1 和 2;同理,此元素的直接后继是 4 ,后继元素也有 2 个,分别是 4 和 5。
2.2顺序表
2.2.1顺序表概述
顺序表的顺序存储是指用一组地址连续的存储单元依次存储线性表中的各个元素,使得线性表在逻辑结构上相邻的元素存储在连续的物理存储单元中,即:通过数据元素物理存储的连续性来反应元素之间逻辑上的相邻关系。采用顺序存储结构存储的线性表通常简称为顺序表。一般情况下采用数组存储。在数组上完成数据的增删查改。
顺序存储的线性表的特点:
- 顺序表的逻辑顺序与物理顺序一致;
- 数据元素之间的关系是以元素在计算机内“物理位置相邻”来体现。
数组实现顺序表的存储结构时,一定要注意预先申请足够大的内存空间,避免因存储空间不足,造成数据溢出,导致不必要的程序错误甚至崩溃。
2.2.2顺序表的存储示意图
顺序表的线性存储示意图如下所示:
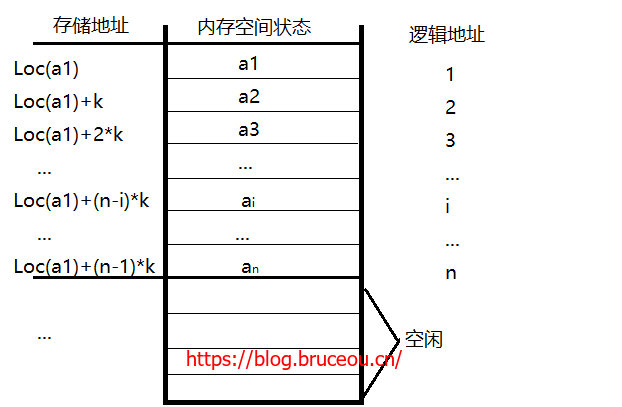
假设线性表中有n个元素,每个元素占k个存储单元,第一个元素的地址为Loc(a1),则第i个元素的地址Loc(ai):
Loc(ai) = Loc(a1) + (i-1) * k;
其中Loc(a1)称为基地址。
2.2.3顺序表实现
顺序表存储结构实现
#define MAX 100
typedef int data_t;
typedef struct _SEQLIST_
{
data_t data[MAX];
int size;
}seqlist_t;【注】顺序表也可以通过指针实现。
data_t是数据元素类型,可以根据需要定义,可以使用seqlist_t定义数据表类型变量。
顺序表的基本操作
(1) 顺序表的初始化
顺序表的初始化就是把顺序表初始化为空的顺序表;只需把顺序表的长度size置为-1即可;
seqlist_t *seqlist_create()
{
seqlist_t *list = NULL;
list = (seqlist_t *)malloc(sizeof(seqlist_t));
if (NULL != list)
{
list->size = -1;//list->size初始化,空表中,list->size = -1;
}
else
{
printf("malloc failed!\n");
return NULL;
}
return list;
}(2) 顺序表判断是否为空
顺序表是否为空,只需判断size的大小是否为-1即可。
int seqlist_is_empty(seqlist_t *list)
{
if(list == NULL)
{
return -1;
}
if (list->size == -1)
{
return 1;
}
else
{
return 0;
}
}(3) 顺序表判断是否为满
顺序表是否为满,只需判断size的大小是否为MAX-1即可。
int seqlist_is_full(seqlist_t *list)
{
if (list == NULL)
{
return -1;
}
if (MAX - 1 == list->size)
{
return 1;
}
else
{
return 0;
}
}(4) 顺序表清空
顺序表清空只需要将size置为-1即可。
void seqlist_clear(seqlist_t *list)
{
if (list == NULL)
{
return ;
}
list->size = -1;//清空线性表
}(5) 求顺序表长度
顺序表的长度就是就顺序表中的元素的个数,由于在插入和删除操作中都有对数据表的长度进行修改,所以求表长只需返回size的值即可;
int seqlist_length(seqlist_t *list)
{
if (list == NULL)
{
return -1;
}
else
{
return (list->size + 1);
}
}(6) 顺序表插入
在数据表的第at个位置插入元素,在顺序表的第at个位置插入元素data,首先将顺序表第at个位置的元素依次向后移动一个位置,然后将元素data插入第at个位置,移动元素要从后往前移动元素,即:先移动最后一个元素,在移动倒数第二个元素,依次类推;插入元素之前要判断插入的位置是否合法,顺序表是否已满,在插入元素之后要将表长加1。
int seqlist_insert(seqlist_t *list, data_t data, int at)
{
/*判断表是否为满*/
if (seqlist_is_full(list))
{
printf("list is full, can't insert!\n");
return -1;
}
/*判断插入位置是否正确*/
if ((at < 0) || (at > MAX-1))
{
printf("at invalid!\n");
return -1;
}
/*判断插入的位置,进行移位*/
int i;
for (i = list->size+1; i > at; i--)
{
list->data[i] = list->data[i-1];
}
/*插入元素*/
list->data[at] = data;
/*表位指针向后移动一位*/
list->size++;
return 0;
}(7) 顺序表删除
删除表中的第at个元素data,删除数据表中的第at个元素,需要将表中第at个元素之后的元素依次向前移动一位,将前面的元素覆盖掉。移动元素时要想将第at+1个元素移动到第at个位置,在将第at+2个元素移动at+1的位置,直到将最后一个元素移动到它的前一个位置,进行删除操作之前要判断顺序表是否为空,删除元素之后,将表长size-1。
int seqlist_at_delete(seqlist_t *list, int at)
{
if(seqlist_is_empty(list))
{
printf("The list is empty!\n");
}
/*判断位置是否有效*/
if ((list == NULL) || (at < 0) || (at > list->size))
{
printf("at invalid!\n");
return -1;
}
/*移动表内元素*/
int i;
for (i = at; i < list->size; i++)
{
list->data[i] = list->data[i+1];
}
/*表尾指针向前移动一位*/
list->size--;
return 0;
}(8) 顺序表查找数据
查找数据有两种,一种是通过位置查找,一种是通过内容查找。
data_t seqlist_at_search(seqlist_t *list, int at)
{
/*判断查询位置是否符合条件*/
if ((at < 0) || (at > list->size))
{
printf("at invalid!\n");
return -1;
}
/*返回查询到的数据*/
return list->data[at];
}int seqlist_data_search(seqlist_t *list, data_t data)
{
/*遍历顺序表,比较值是否等于data*/
int i;
for (i = 0; i < list->size+1; i++)
{
if (data == list->data[i])
{
return i;
}
}
return -1;
}(9) 顺序表修改数据
顺序表修改数据有两种,一种是通过位置修改,一种是通过内容修改。
int seqlist_at_change(seqlist_t *list, data_t data, int at)
{
/*判断位置是否有效*/
if ((list == NULL) || (at < 0) || (at > list->size))
{
printf("at invalid!\n");
return -1;
}
/*修改该位置的值*/
list->data[at] = data;
return 0;
}int seqlist_data_change(seqlist_t *list, data_t old_data, data_t new_data)
{
/*判断old_data是否存在,得到数据的位置*/
#if 1
int at;
int i;
for (i = 0; i < list->size+1; i++)
{
if (old_data == list->data[i])
{
at = i;
}
}
/*修改该位置的值*/
list->data[at] = new_data;
#else
int at = seqlist_data_search(list, old_data);
if (-1 == at)
{
printf("no such data!\n");
return -1;
}
list->data[at] = new_data;
#endif
return 0;
}(10) 顺序表打印数据
打印数据就很简单了,一次取出数据即可。
void seqlist_show(seqlist_t *list)
{
int i;
int j = 0;
for (i = 0; i < list->size+1; i++)
{
if(j == 10)
{
printf("\n");
}
++j;
printf("%6d", list->data[i]);
}
printf("\n");
}(11) 释放顺序表
void seqlist_destroy(seqlist_t *list)
{
if (list == NULL)
{
return ;
}
free(list);
return;
}【完整代码参考2.1 seqlist】
2.3 单链表
2.3.1单链表概述
前面讲解了顺序表,接下来讲解链表。既然有顺序表为何又有链表呢?在操作顺序表的时候插入和删除最坏的情况是O(N)。引入链表就是为了避免插入和删除的线性开销,链表可以不连续存储,链表和顺序表应用场景不同,在查找等场合使用顺序表较快,而在插入和删除的场合使用链表较好。
链表就是典型的链式存储,将线性表L =(a0,a1,a2,……..an-1)中个元素分布在存储器的不同存储块,成为结点(Node),通过地址或指针建立他们之间的联系,所得到的存储结构为链表结构。
链表是一系列的存储数据元素的单元通过指针串接起来形成的,因此每个单元至少有两个域,
一个域用于数据元素的存储,另一个域是指向其他单元的指针。这里具有一个数据域和多个指针域的存储单元通常称为结点(node)。
2.3.2单链表的存储示意图
链表中每个数据的存储都由以下两部分组成:
- 数据元素本身,其所在的区域称为数据域;
- 指向直接后继元素的指针,所在的区域称为指针域;
即链表中存储各数据元素的结构如图所示:

上图所示的结构在链表中称为节点。也就是说,链表实际存储的是一个一个的节点,真正的数据元素包含在这些节点中,如图所示:

一个完整的链表需要由以下几部分构成:
1.头指针:一个普通的指针,它的特点是永远指向链表第一个节点的位置。很明显,头指针用于指明链表的位置,便于后期找到链表并使用表中的数据;
2.节点:链表中的节点又细分为头节点、首元节点和其他节点:
- 头节点:其实就是一个不存任何数据的空节点,通常作为链表的第一个节点。对于链表来说,头节点不是必须的,它的作用只是为了方便解决某些实际问题;
- 首元节点:由于头节点(也就是空节点)的缘故,链表中称第一个存有数据的节点为首元节点。首元节点只是对链表中第一个存有数据节点的一个称谓,没有实际意义;
- 其他节点:链表中其他的节点。
因此,一个存储 {1,2,3}的完整链表结构如图所示:
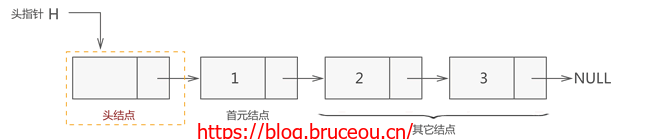
注意:链表中有头节点时,头指针指向头节点;反之,若链表中没有头节点,则头指针指向首元节点。
上文提到链表中可以有头结点也可以没有头结点,那么有头结点有何好处呢?在回答问题之前我们先看看在实际工作中可能出现的的问题。首先,并不存在从定义出发在表的前面插入元素的真正显性方法。第二,从表的前面实行删除是一个特殊情况,因为它改变了表的起始端;编程中的疏忽将会引起表的丢失。第三,虽然上述指针的移动很简单,但是删除算法要求我们记住删除元素前面的表元。为此,我们通过一个简单的改变来解决以上问题,我们将留出一个标志节点,有时称为表头(header)或哑结点(dummy node),这就是上图所示一个带有头结点的单链表。
参见《数据结构与算法分析:C语言描述》第3.2.3节
以上这段话很重要,回答了为何要带有头结点。
2.3.3单链表实现
单链表存储结构实现
typedef int data_t;
typedef struct linklist_node_t
{
data_t data;
struct linklist_node_t *next;
}linklist_t;单链表的基本操作
(1) 单链表的初始化
单链表的初始化就是把单链表初始化为空的链表;只需把单链表的头节点数据置为-1即可;
linklist_t *linklist_create()
{
linklist_t *head = (linklist_t *)malloc(sizeof(linklist_t));
if (NULL == head)
{
printf("malloc failed!\n");
return NULL;
}
else
{
head->data = -1;
head->next = NULL;
}
return head;
}(2) 单链表判断是否为空
单链表是否为空,只需判断head->next是否为NULL即可。
int linklist_is_empty(linklist_t *head)
{
if (NULL != head)
{
if (NULL == head->next)
{
return 1;
}
else
{
return 0;
}
}
else
{
return -1;
}
}(3) 求单链表长度
求单链表长度,只需要不断判断next节点是否为空,如果不为NULL则加1,最后返回长度即可。
int linklist_length(linklist_t *head)
{
linklist_t *p;
int len = 0;
if(head == NULL)
{
return -1;
}
p = (linklist_t *)head->next;
while (p != NULL)
{
len++;
p = (linklist_t *)p->next;
}
return len;
}(4) 单链表清空
清空单链表,从首节点开始以此清除后面的节点即可。
void linklist_clear(linklist_t *head)
{
linklist_t *p = (linklist_t *)head->next;
linklist_t *q = NULL;
if (NULL == head)
{
return ;
}
#if 1
while (q != NULL)
{
q = (linklist_t *)p->next;
free(p);
p = q;
}
#else
while (head->next != NULL)
{
q = (linklist_t *)head->next;
head->next = head->next->next;
free(q);
}
#endif
head->next = NULL;
}(5) 单链表插入数据
同顺序表一样,向链表中增添元素,根据添加位置不同,可分为以下 3 种情况:
- 插入到链表的头部(头节点之后),作为首元节点;
- 插入到链表中间的某个位置;
- 插入到链表的最末端,作为链表中最后一个数据元素;
虽然新元素的插入位置不固定,但是链表插入元素的思想是固定的,只需做以下两步操作,即可将新元素插入到指定的位置:
步骤1:将新结点的 next 指针指向插入位置后的结点;
步骤2:将插入位置前结点的 next 指针指向插入结点;
例如,我们在链表 {1,2,3,4} 的基础上分别实现在头部、中间部位、尾部插入新元素 5,其实现过程如图所示:
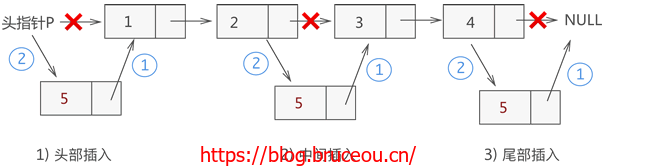
从图中可以看出,虽然新元素的插入位置不同,但实现插入操作的方法是一致的,都是先执行步骤 1 ,再执行步骤 2。
注意:链表插入元素的操作必须是先步骤 1,再步骤 2;反之,若先执行步骤 2,除非再添加一个指针,作为插入位置后续链表的头指针,否则会导致插入位置后的这部分链表丢失,无法再实现步骤 1。
下面就是一个具体链表的插入过程图。
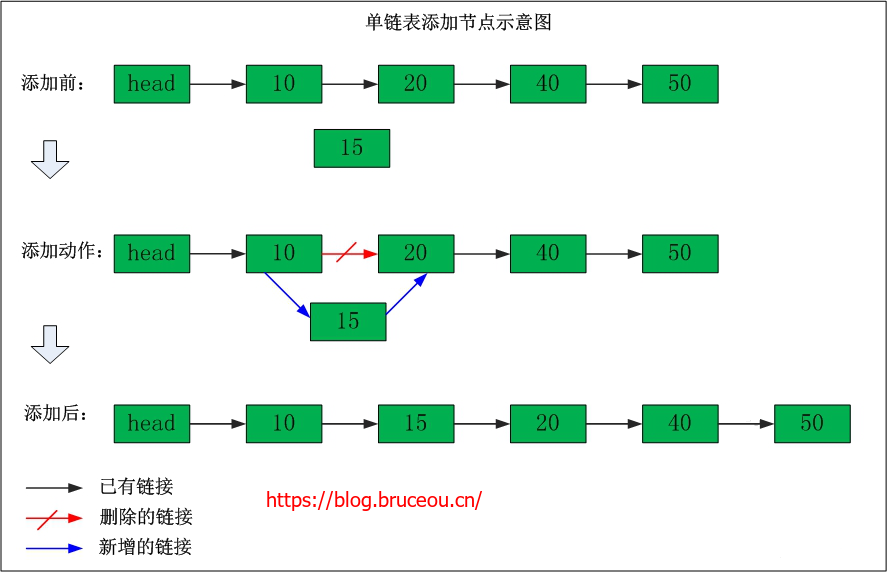
int linklist_insert(linklist_t *head, data_t data, int at)
{
if (NULL == head)
{
return -1;
}
/*判断位置是否正确*/
int len = linklist_length(head);
if ((at < 0) || (at > len))
{
printf("at invalid!\n");
return -1;
}
/*给数据开辟结点空间*/
linklist_t *p = (linklist_t *)malloc(sizeof(linklist_t));
if (NULL == p)
{
printf("malloc failed!\n");
return -1;
}
p->data = data;
p->next = NULL;
linklist_t *q = head;
int i;
/*找到插入位置的前一个位置*/
for (i = 0; i < at; i++)
{
q = (linklist_t *)q->next;
}
/*插入元素*/
p->next = q->next;//将新结点的 next 指针指向插入位置后的结点;
q->next = p;//将插入位置前结点的 next 指针指向插入结点
return 0;
}(6) 单链表删除数据
从链表中删除指定数据元素时,实则就是将存有该数据元素的节点从链表中摘除,但作为一名合格的程序员,要对存储空间负责,对不再利用的存储空间要及时释放。因此,从链表中删除数据元素需要进行以下 2 步操作:
步骤1:将结点从链表中摘下来;
步骤2:手动释放掉结点,回收被结点占用的存储空间;
其中,从链表上摘除某节点的实现非常简单,只需找到该节点的直接前驱节点 temp,执行一行程序: 例如,从存有 的链表中删除元素 3,则此代码的执行效果如图所示:

下面就是一个具体链表的删除过程图。
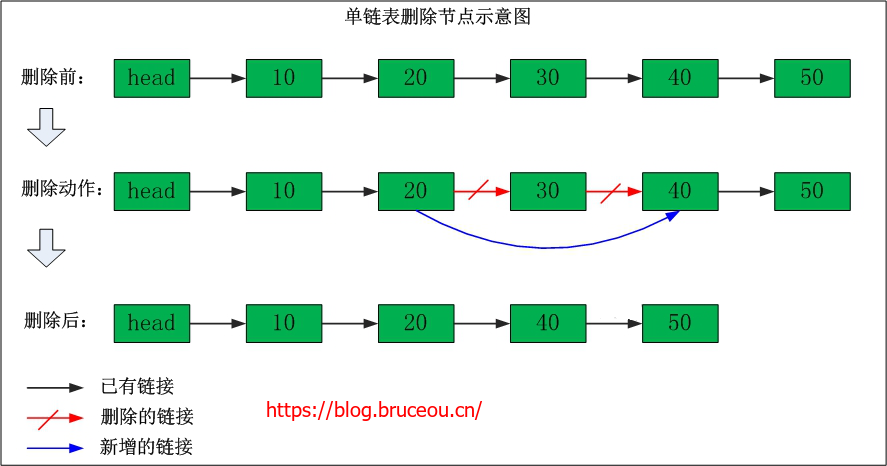
int linklist_at_delete(linklist_t *head, int at)
{
int len = linklist_length(head);
if ((at < 0) || (at > len-1))
{
printf("at invalid!\n");
return -1;
}
linklist_t *temp = head;
int i;
//保存第一个元素节点的位置
for (i = 0; i < at; i++)
{
temp = temp->next;
}
linklist_t *q = temp->next;//单独设置一个指针指向被删除结点,以防丢失
//方法一
//temp->next = q->next;
//方法二:此方法更容易理解
temp->next = temp->next->next;//删除某个结点的方法就是更改前一个结点的指针域
free(q);
q = NULL;
return 0;
}(7) 单链表查找数据
查找数据有两种,一种是通过位置查找,一种是通过内容查找。
data_t linklist_at_search(linklist_t *head, int at)
{
int offset=-1;
int len = linklist_length(head);
if ((at < 0) || (at > len))
{
printf("at invalid!\n");
return -1;
}
linklist_t *p = head->next;
int i;
for (i = 0; i < at; i++)
{
offset++;
if (offset == at)
{
return p->data;
}
p=p->next;
}
return p->data;
}int linklist_data_search(linklist_t *head, data_t data)
{
linklist_t *p = head->next;
int at=-1;
while (p!= NULL)
{
at++;
if (p->data == data)
{
return at;
}
p=p->next;
}
return -1;
}(8) 单链表修改数据
修改数据有两种,一种是通过位置查找,一种是通过内容查找。
int linklist_at_change(linklist_t *head, data_t data, int at)
{
linklist_t *p=head;
int len=linklist_length(head);
if ((at < 0) || (at > len))
{
printf("at invalid!\n");
return -1;
}
int i;
for (i = 0; i < at; i++)
{
p = p->next;
}
p->data=data;
return 0;
}int linklist_data_change(linklist_t *head, data_t old_data, data_t new_data)
{
if(head == NULL)
{
return -1;
}
linklist_t *p=head->next;
int at=linklist_data_search(head, old_data);
if(at == -1)
{
return -1;
}
int i;
for (i = 0; i < at; i++)
{
p = p->next;
}
p->data=new_data;
return 0;
}(9) 单链表打印数据
打印数据就简单了,以此遍历即可。
void linklist_show(linklist_t *head)
{
linklist_t *p = head->next;
while (p != NULL)
{
printf("%d, ", p->data);
p = p->next;
}
printf("\n");
}(10) 释放单链表
释放单链表前先清除数据。
void linklist_destroy(linklist_t **head)
{
if(linklist_is_empty(*head) != 1)
{
linklist_clear(*head);
}
free(*head);
*head = NULL;
}好了,以上就是单链表的基本操作。
【完整代码参考2.2 linklist】
2.4 循环链表
2.4.1循环链表概述
前面我们学习了单向链表,现在介绍单向循环链表,单向循环链表是单链表的一种改进,若将单链表的首尾节点相连,便构成单向循环链表结构,如下图:

对于一个循环链表来说,其首节点和末节点被连接在一起。这种方式在单向和双向链表中皆可实现。要转换一个循环链表,可以选择开始于任意一个节点然后沿着列表的任一方向直到返回开始的节点。再来看另一种方法,循环链表可以被视为“无头无尾”。这种列表很利于节约数据存储缓存, 假定你在一个列表中有一个对象并且希望所有其他对象迭代在一个非特殊的排列下。指向整个列表的指针可以被称作访问指针。
循环链表中第一个节点之前就是最后一个节点,反之亦然。循环链表的无边界使得在这样的链表上设计算法会比普通链表更加容易。对于新加入的节点应该是在第一个节点之前还是最后一个节点之后可以根据实际要求灵活处理,区别不大。当然,如果只会在最后插入数据(或者只会在之前),处理也是很容易的。
2.4.2循环链表实现
循环链表存储结构实现
typedef int data_t;
typedef struct cyclinklist_node_t
{
data_t data;
struct cyclinklist_node_t *next;
}cyclinklist_t;循环链表的基本操作
/**
******************************************************************************
* @file cyclinklist.c
* @author BruceOu
* @version V1.0
* @date 2019.06.14
* @brief 循环链表 API
******************************************************************************
*/
/**Includes*********************************************************************/
#include "cyclinklist.h"
/**
* @brief 创建循环链表函数
* @param None
* @retval head
*/
cyclinklist_t *cyclinklist_create()
{
cyclinklist_t *head = (cyclinklist_t *)malloc(sizeof(cyclinklist_t));
if (NULL == head)
{
printf("malloc failed!\n");
return NULL;
}
else
{
head->data = -1;
head->next = head;//这里的尾指针指向头部
}
return head;
}
/**
* @brief 判断循环链表是否为空
* @param None
* @retval 返回1表示为空,返回0表示不为空,失败返回-1
*/
int cyclinklist_is_empty(cyclinklist_t *head)
{
if (NULL != head)
{
return (head == head->next);
}
else
{
return -1;
}
}
/**
* @brief 求链表长度
* @param head
* @retval 成功返回链表长度,失败返回-1
*/
int cyclinklist_length(cyclinklist_t *head)
{
cyclinklist_t *p;
int len = 0;
if(head == NULL)
{
return -1;
}
p = head->next;
while (p != head)
{
len++;
p = p->next;
}
return len;
}
/**
* @brief 清除链表
* @param head
* @retval None
*/
void cyclinklist_clear(cyclinklist_t *head)
{
cyclinklist_t *p = (cyclinklist_t *)head->next;
cyclinklist_t *q = NULL;
if (NULL == head)
{
return;
}
while (p != head)
{
//q = (cyclinklist_t *)p;//暂存next节点
//p = p->next;
//free(q);//释放要删除的内存空间节点
q = p->next;
free(p);
p = q;
}
head->next = head;
}
/**
* @brief 在循环链表中插入数据
* @param head 当前操作的链表
data 插入的数据
at 插入的位置
* @retval 成功返回0,失败返回-1
*/
int cyclinklist_insert(cyclinklist_t *head, data_t data, int at)
{
if (NULL == head)
{
return -1;
}
/*判断位置是否正确*/
if (at < 0)
{
printf("at invalid!\n");
return -1;
}
/*给数据开辟结点空间*/
cyclinklist_t *p = (cyclinklist_t *)malloc(sizeof(cyclinklist_t));
if (NULL == p)
{
printf("malloc failed!\n");
return -1;
}
p->data = data;
p->next = NULL;
/*找到插入位置的前一个位置*/
cyclinklist_t *q = head;
int i;
for (i = 0; i < at; i++)
{
q = q->next;
}
/*插入元素*/
p->next = q->next;
q->next = p;
return 0;
}
/**
* @brief 在链表中删除指定数据
* @param head 当前操作的链表
data 要删除的数据
* @retval 成功返回0,失败返回-1
*/
int cyclinklist_data_delete(cyclinklist_t *head, data_t data)
{
/*查询需要删除数据的前一个位置*/
#if 0
int at = cyclinklist_data_search(head, data);
if (-1 == at)
{
printf("no such data!\n");
return -1;
}
cyclinklist_t *p = head;
int i;
for (i = 0; i < offset; i++)
{
p = p->next;
}
#else
cyclinklist_t *p = head;
while (p->next != head)
{
if (p->next->data == data)
{
break;
}
p = p->next;
}
if (p->next == head)
{
return -1;
}
#endif
/*删除这个位置*/
cyclinklist_t *q = p->next;
p->next = q->next;
free(q);
q = NULL;
return 0;
}
/**
* @brief 在链表中删除指定位置数据
* @param head 当前操作的链表
at 要删除的数据位置
* @retval 成功返回0,失败返回-1
*/
int cyclinklist_at_delete(cyclinklist_t *head, int at)
{
cyclinklist_t *p = head;
int i;
for (i = 0; i < at; i++)
{
p = p->next;
if (p->next == head)
{
p = p->next;
}
}
cyclinklist_t *q = p->next;
//方法一
//p->next = q->next;
//方法二
p->next = p->next->next;
free(q);
q = NULL;
return 0;
}
/**
* @brief 在链表中修改数据
* @param head 当前操作的链表
old_data 要修改的数据
new_data 修改后的数据
* @retval 成功返回0,失败返回-1
*/
int cyclinklist_data_change(cyclinklist_t *head, data_t old_data, data_t new_data)
{
cyclinklist_t *p = head->next;
while (p != head)
{
if (p->data == old_data)
{
p->data = new_data;
return 0;
}
p = p->next;
}
return -1;
}
/**
* @brief 在链表中修改指定位置数据
* @param head 当前操作的链表
data 修改后的数据
at 数据的位置
* @retval 成功返回0,失败返回-1
*/
int cyclinklist_at_change(cyclinklist_t *head, data_t data, int at)
{
cyclinklist_t *p = head->next;
int i;
for (i = 0; i < at; i++)
{
p = p->next;
if (p == head)
{
p = p->next;
}
}
p->data = data;
return 0;
}
/**
* @brief 在链表中查找数据
* @param head 当前操作的链表
data 要查找的数据
* @retval 成功返回查找数据的位置,失败返回-1
*/
int cyclinklist_data_search(cyclinklist_t *head, data_t data)
{
cyclinklist_t *p = head->next;
int at = -1;
while (p != head)
{
at++;
if (data == p->data)
{
return at;
}
p = p->next;
}
return -1;
}
/**
* @brief 在链表中查找指定位置数据
* @param head 当前操作的链表
at 要查找指定位置
* @retval 成功返回0,失败返回-1
*/
data_t cyclinklist_at_search(cyclinklist_t *head, int at)
{
cyclinklist_t *p = head->next;
int i;
for (i = 0; i < at; i++)
{
p = p->next;
if (p == head)
{
p = p->next;
}
}
return p->data;
}
/**
* @brief 在链表中打印数据
* @param head 当前操作的链表
* @retval None
*/
void cyclinklist_show(cyclinklist_t *head)
{
cyclinklist_t *p = head->next;
while (p != head)
{
printf("%d, ", p->data);
p = p->next;
}
printf("\n");
}
/**
* @brief 回收链表
* @param head 当前操作的链表
* @retval None
*/
void cyclinklist_destroy(cyclinklist_t **head)
{
if(cyclinklist_is_empty(*head) != 1)
{
cyclinklist_clear(*head);
}
free(*head);
*head = NULL;
}
/**
* @brief 反转链表
* @param head 当前操作的链表
* @retval None
*/
void cyclinklist_invert(cyclinklist_t *head)
{
cyclinklist_t *p = head;
cyclinklist_t *q = head->next;
p->next = head;
cyclinklist_t *t = NULL;
while (q != head)
{
t = q->next;
q->next = p->next;
p->next = q;
q = t;
}
}#ifndef _CYCLINKLIST_H_
#define _CYCLINKLIST_H_
#include <stdio.h>
#include <malloc.h>
#include <stdlib.h>
#include <strings.h>
typedef int data_t;
typedef struct cyclinklist_node_t
{
data_t data;
struct cyclinklist_node_t *next;
}cyclinklist_t;
cyclinklist_t *cyclinklist_create();//创建循环链表
int cyclinklist_is_empty(cyclinklist_t *head);//判断是否为空
int cyclinklist_length(cyclinklist_t *head);//求长度
void cyclinklist_clear(cyclinklist_t *head);//清除数据
int cyclinklist_insert(cyclinklist_t *head, data_t data, int at);//插入数据
int cyclinklist_data_delete(cyclinklist_t *head, data_t data);//删除指定数据
int cyclinklist_at_delete(cyclinklist_t *head, int at);//删除指定位置数据
int cyclinklist_data_change(cyclinklist_t *head, data_t old_data, data_t new_data);//改变指定数据
int cyclinklist_at_change(cyclinklist_t *head, data_t data, int at);//改变指定位置数据
int cyclinklist_data_search(cyclinklist_t *head, data_t data);//查找指定数据
data_t cyclinklist_at_search(cyclinklist_t *head, int at);//查找指定位置数据
void cyclinklist_show(cyclinklist_t *head);//打印数据
void cyclinklist_destroy(cyclinklist_t **head);//回收空间
#endif判断链表是不是循环链表
判断是否是循环链表时,也设置两个指针,慢指针和快指针,让快指针比慢指针每次移动快两次。如果快指针追赶上慢指针,则为循环链表,否则不是循环链表,如果快指针或者慢指针指向NULL,则不是循环链表。
int JudgeIsloop(cyclinklist_t *head)
{
int flag = 0;
cyclinklist_t *slow,*fast;
if(head == NULL)
{
return 0;
}
slow = head;
fast = head->next;
while(slow)
{
if(fast == NULL || fast->next == NULL)//走到头了
{
return 0;
}
else if(fast == slow || fast->next == slow)//二者相遇,因为fast走的快,如果fast->next指向slow,也是循环的
{
flag = 1;
return 1;
}
else
{
slow = slow->next;//慢指针走一步
fast = fast->next->next;//快指针走两步
}
}
return 0;
}【完整代码参考附件2.3cyclinklist】
| 举一反三 |
【练一练】
【1、单向链表回文判断】
判断一条单向链表是不是“回文” 。
【分析与解答】
【解法一:栈(数组)方法】
这个判断回文字符串类似,我们可以先将数据存储在数组或者栈中,然后取出数据和原单链表进行比较。对于C语言来说,没有现成的栈的数据结构,可以自己实现,对于C++,可以调用STL中的栈。
bool isPalindrome(linklist_t *head)
{
linkstack *stack = CreateEmptyLinkstack();
linklist_t *p1 = head->next;
while (p1 != NULL)
{
PushLinkstack(stack, p1->data);
p1 = p1->next;
}
linklist_t *p2 = head->next;
int x;
//判断是否回文
while(p2->next !=NULL && EmptyLinkstack(stack) != 1)
{
x = GetTopLinkstack(stack);//取栈顶元素
PopLinkstack(stack);//出栈
if(x != p2->data)
{
return false;
}
p2=p2->next;
}
ClearLinkstack(stack);
if(EmptyLinkstack(stack))
{
printf("The linkstack is empty!\n");
}
Destroylinkstack(stack) ;
return true;
}当然还可以进行优化,借助一个栈存放前半段的元素,然后和后半段的比较。最后的时间复杂度也可达到O(N)。
bool isPalindrome(linklist_t *head)
{
linkstack *stack = CreateEmptyLinkstack();
linklist_t *p1 = head->next;
linklist_t *p2 = head->next;
while (p1 != NULL && p2 != NULL)
{
PushLinkstack(stack, p1->data);
p1 = p1->next;
p2 = p2->next->next;
}
int x;
//判断是否回文
while(p1->next !=NULL && EmptyLinkstack(stack) != 1)
{
x = GetTopLinkstack(stack);//取栈顶元素
PopLinkstack(stack);//出栈
if(x != p1->data)
{
return false;
}
p1=p1->next;
}
ClearLinkstack(stack);
if(EmptyLinkstack(stack))
{
printf("The linkstack is empty!\n");
}
Destroylinkstack(stack) ;
return true;
}【解法二:快慢指针法】
对于单链表结构,可以用两个指针从两端或者中间遍历并判断对应字符是否相等。但这里的关键就是如何朝两个方向遍历。由于单链表是单向的,所以要向两个方向遍历的话,可以采取经典的快慢指针的方法,即先定位到链表的中间位置,再将链表的后半逆置,最后用两个指针同时从链表头部和中间开始同时遍历并比较即可。
【注】此种方法对于无头结点的链表比较适用,和解法一的改进也比较类似,只是解法一的改进空间复杂度比此方法高,请读者朋友自行思考吧。
【2、有序链表合并】
将两个有序链表合并为一个新的有序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例:
输入:
1->2->4
1->3->4
输出:
1->1->2->3->4->4
【分析与解答】
【解法一:非递归】
首先我们使用非递归的方法,其步骤如下:
(1)对空链表存在的情况进行处理,假如 pHead1 为空则返回 pHead2 ,pHead2 为空则返回 pHead1。(两个都为空此情况在pHead1为空已经被拦截)
(2)在两个链表无空链表的情况下确定第一个结点,比较链表1和链表2的第一个结点的值,将值小的结点保存下来为合并后的第一个结点。并且把第一个结点为最小的链表向后移动一个元素。
(3)继续在剩下的元素中选择小的值,连接到第一个结点后面,并不断next将值小的结点连接到第一个结点后面,直到某一个链表为空。
(4)当两个链表长度不一致时,也就是比较完成后其中一个链表为空,此时需要把另外一个链表剩下的元素都连接到第一个结点的后面。
linklist_t *mergeTwoOrderedLists(linklist_t* pHead1, linklist_t* pHead2)
{
linklist_t* pTail = NULL;//指向新链表的最后一个结点 pTail->next去连接
linklist_t* newHead = NULL;
if (NULL == pHead1->next)
{
return pHead2;
}
else if(NULL == pHead2->next)
{
return pHead1;
}
else
{
//确定头指针
if ( pHead1->next->data < pHead2->next->data)
{
newHead = pHead1;
pHead1 = pHead1->next;//指向链表的第二个结点
pHead2 = pHead2->next;
}
else
{
newHead = pHead2;
pHead1 = pHead1->next;
pHead2 = pHead2->next;
}
pTail = newHead;//指向第一个结点
while ( pHead1 && pHead2)
{
if ( pHead1->data <= pHead2->data )
{
pTail->next = pHead1;
pHead1 = pHead1->next;
}
else
{
pTail->next = pHead2;
pHead2 = pHead2->next;
}
pTail = pTail->next;
}
if(NULL == pHead1)
{
pTail->next = pHead2;
}
else if(NULL == pHead2)
{
pTail->next = pHead1;
}
return newHead;
}
}【解法二:递归方法】
递归方法步骤如下:
(1)对空链表存在的情况进行处理,假如 pHead1 为空则返回 pHead2 ,pHead2 为空则返回 pHead1。
(2)比较两个链表第一个结点的大小,确定头结点的位置
(3)头结点确定后,继续在剩下的结点中选出下一个结点去链接到第二步选出的结点后面,然后在继续重复(2 )(3) 步,直到有链表为空。
linklist_t *mergeTwoOrderedLists(linklist_t* pHead1, linklist_t* pHead2)
{
linklist_t* newHead = NULL;
if (NULL == pHead1)
{
return pHead2;
}
else if(NULL ==pHead2)
{
return pHead2;
}
else
{
if (pHead1->data < pHead2->data)
{
newHead = pHead1;
newHead->next = mergeTwoOrderedLists(pHead1->next, pHead2);
}
else
{
newHead = pHead2;
newHead->next = mergeTwoOrderedLists(pHead1, pHead2->next);
}
return newHead;
}
}【3、使用链表实现大数加法】
两个用链表代表的整数,其中每个节点包含一个数字。数字存储按照在原来整数中相反的顺序,使得第一个数字位于链表的开头。写出一个函数将两个整数相加,用链表形式返回和。
示例:
输入:
3->1->5
5->9->2
输出:
8->0->8
【分析与解答】
很简单,只是在两数之和大于10时要进位,代码如下所示:
linklist_t* numberAddAsList(linklist_t* l1, linklist_t* l2)
{
linklist_t *ret = l1, *pre = l1;
int up = 0;
while (l1 != NULL && l2 != NULL)
{
//数值相加
l1->data = l1->data + l2->data + up;
//计算是否有进位
up = l1->data / 10;
//保留计算结果的个位
l1->data %= 10;
//记录当前节点位置
pre = l1;
//同时向后移位
l1 = l1->next;
l2 = l2->next;
}
//若l1到达末尾,说明l1长度小于l2
if (l1 == NULL)
//pre->next指向l2的当前位置
pre->next = l2;
//l1指针指向l2节点当前位置
l1 = pre->next;
//继续计算剩余节点
while (l1 != NULL)
{
l1->data = l1->data + up;
up = l1->data / 10;
l1->data %= 10;
pre = l1;
l1 = l1->next;
}
//最高位计算有进位,则新建一个节点保留最高位
if (up != 0)
{
linklist_t *tmp = (linklist_t *)malloc(sizeof(linklist_t));
pre->next = tmp;
}
//返回计算结果链表
return ret;
}【4、查找链表中倒数第k个结点】
输入一个单向链表,输出该链表中倒数第k个结点。链表的倒数第0个结点为链表的尾指针。
链表结点定义如下:
typedef int data_t;
typedef struct linklist_node_t
{
data_t data;
struct linklist_node_t *next;
}linklist_t;提示:设置一前一后两个指针,一个指针步长为1,另一个指针步长为k,当一个指针走到链表尾端时,另一指针指向的元素即为链表倒数第k个元素。
【分析与解答】
【解法一:两次遍历法】
为了得到倒数第k个结点,很自然的想法是先走到链表的尾端,再从尾端回溯k步。可是输入的是单向链表,只有从前往后的指针而没有从后往前的指针。因此我们需要打开我们的思路。
既然不能从尾结点开始遍历这个链表,我们还是把思路回到头结点上来。假设整个链表有n个结点,那么倒数第k个结点是从头结点开始的第n-k-1个结点(从0开始计数)。如果我们能够得到链表中结点的个数n,那我们只要从头结点开始往后走n-k-1步就可以了。如何得到结点数n?这个不难,只需要从头开始遍历链表,每经过一个结点,计数器加一就行了。
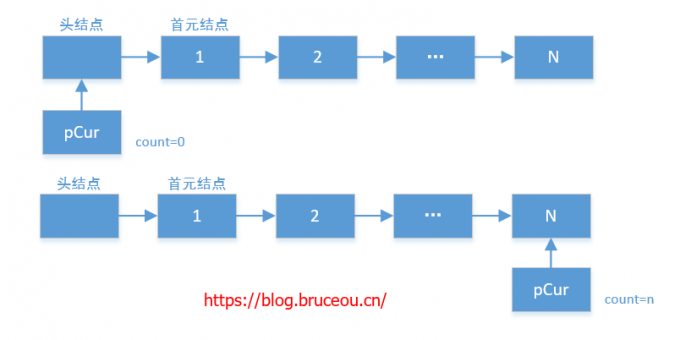
这种思路的时间复杂度是O(n),但需要遍历链表两次。第一次得到链表中结点个数n,第二次得到从头结点开始的第n-k个结点即倒数第k个结点。
int num;//定义num值
linklist_t* FindKthToTail_Solution(linklist_t* pListHead, unsigned int k)
{
num = k;
if(pListHead == NULL)
return NULL;
linklist_t *phead = pListHead;
//递归调用
linklist_t* pCur = FindKthToTail_Solution(phead->next, k);
if(pCur != NULL)
{
return pCur;
}
else
{
num--;// 递归返回一次,num值减1
if(num == 0)
return phead;//返回倒数第K个节点
return NULL;
}
}【解法二:递归法】
我们还可以使用递归的方法,首先定义num = k,然后使用递归方式遍历至链表末尾。然后由末尾开始返回,每返回一次 num 减 1,当 num 为 0 时,即可找到目标节点。
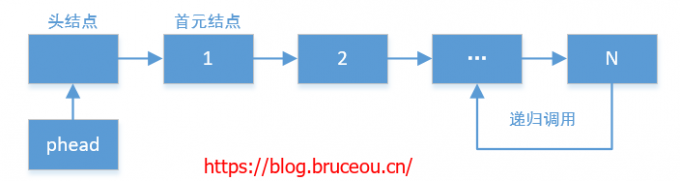
int num;//定义num值
linklist_t* FindKthToTail_Solution(linklist_t* pListHead, unsigned int k)
{
num = k;
if(pListHead == NULL)
return NULL;
//递归调用
linklist_t* pCur = FindKthToTail_Solution(pListHead->next, k);
if(pCur != NULL)
{
return pCur;
}
else
{
num--;// 递归返回一次,num值减1
if(num == 0)
return pListHead;//返回倒数第K个节点
return NULL;
}
}【解法三:双指针法】
如果链表的结点数不多,这是一种很好的方法。但如果输入的链表的结点个数很多,有可能不能一次性把整个链表都从硬盘读入物理内存,那么遍历两遍意味着一个结点需要两次从硬盘读入到物理内存。我们知道把数据从硬盘读入到内存是非常耗时间的操作。我们能不能把链表遍历的次数减少到1?如果可以,将能有效地提高代码执行的时间效率。
如果我们在遍历时维持两个指针,第一个指针从链表的头指针开始遍历,在第k-1步之前,第二个指针保持不动;在第k-1步开始,第二个指针也开始从链表的头指针开始遍历。由于两个指针的距离保持在k-1,当第一个(走在前面的)指针到达链表的尾结点时,第二个指针(走在后面的)指针正好是倒数第k个结点。
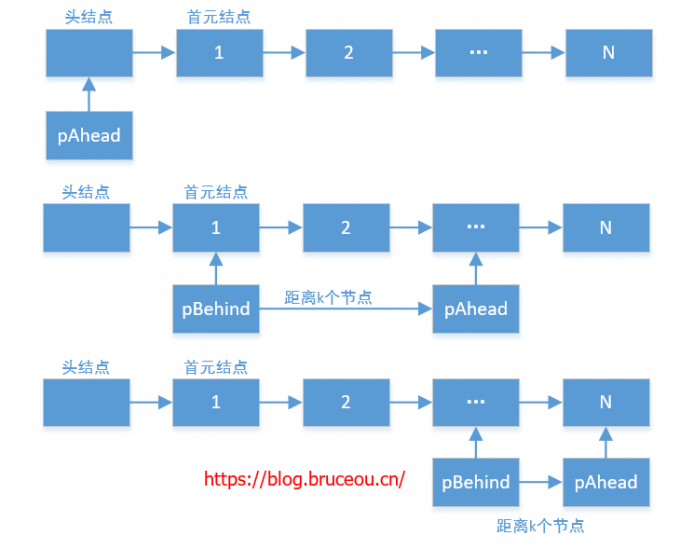
这种思路只需要遍历链表一次。对于很长的链表,只需要把每个结点从硬盘导入到内存一次。因此这一方法的时间效率前面的方法要高。
linklist_t* FindKthToTail_Solution(linklist_t* pListHead, unsigned int k)
{
if(pListHead == NULL)
return NULL;
linklist_t *pAhead = pListHead;
linklist_t *pBehind = NULL;
for(unsigned int i = 0; i < k; ++ i)
{
if(pAhead->next != NULL)
pAhead = pAhead->next;
else
{
// if the number of nodes in the list is less than k,
// do nothing
return NULL;
}
}
pBehind = pListHead->next;
// the distance between pAhead and pBehind is k
// when pAhead arrives at the tail, p
// Behind is at the kth node from the tail
while(pAhead->next != NULL)
{
pAhead = pAhead->next;
pBehind = pBehind->next;
}
return pBehind;
}这道题的代码有大量的指针操作。在软件开发中,错误的指针操作是大部分问题的根源。因此每个公司都希望程序员在操作指针时有良好的习惯,比如使用指针之前判断是不是空指针。这些都是编程的细节,但如果这些细节把握得不好,很有可能就会和心仪的公司失之交臂。
另外,这两种思路对应的代码都含有循环。含有循环的代码经常出的问题是在循环结束条件的判断。是该用小于还是小于等于?是该用k还是该用k-1?由于题目要求的是从0开始计数,而我们的习惯思维是从1开始计数,因此首先要想好这些边界条件再开始编写代码,再者要在编写完代码之后再用边界值、边界值减1、边界值加1都运行一次(在纸上写代码就只能在心里运行了)。
扩展:和这道题类似的题目还有:输入一个单向链表。如果该链表的结点数为奇数,输出中间的结点;如果链表结点数为偶数,输出中间两个结点前面的一个。如果各位感兴趣,请自己分析并编写代码。
代码获取方法
1.关注公众号[嵌入式实验楼]
2.在公众号回复关键词[Data Structures and Algorithms]获取资料提取码

